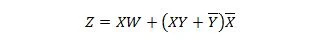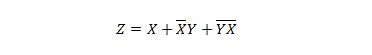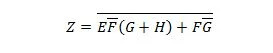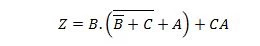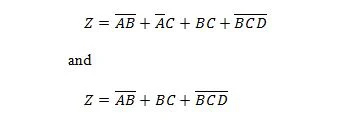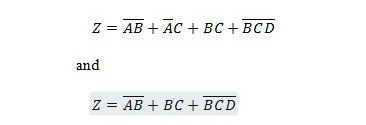פרק 2: אלגברה בוליאנית ורכיבי המחשב הקשורים לה
2.1 אופרטורים בוליאניים בסיסיים
נניח שאני (המחבר) גבוה ואתה (הקורא) גבוה. אם מישהו שואל אותך אם שנינו גבוהים, היית אומר 'כן' (נכון). אם הוא שואל אם שנינו נמוכים, היית אומר 'לא' (שקר). אם אתה נמוך ואני גבוה, והוא שואל אותך אם אתה או אני גבוהים, התשובה שלך תהיה 'כן' (נכון). אם הוא ישאל אם גם אתה וגם אני גבוהים, לא תהיה לך תשובה. אפשר להמשיך ולומר שאסור לשאול את השאלה האחרונה או שאין לשאלה תשובה. ובכן, אני רוצה שתדע (הקורא) שהיום, בנסיבות מסוימות, יש לשאול את השאלה.
בביולוגיה, אדם הוא גבוה או נמוך. התנאים ה'סביבתיים' הם שגורמים לאדם להיות בעל גובה בינוני. מדען אחד, ג'ורג' בול, הגדיר קבוצה של תשובות או כללים לסוג זה של שאלות. נלמד כללים אלה בחלק זה של קורס הקריירה המקוון (פרק). כללים אלה משמשים כיום בתחום המחשוב, התכנות, האלקטרוניקה והטלקומוניקציה. למעשה, ללא הכללים הללו, לא היה לך מחשב, כפי שהוא נפוץ היום; לא תהיה לך גם תכנות, כפי שזה נפוץ היום.
אמת או שקר
הצהרת שפה אנושית פשוטה היא נכונה או שקרית בפני עצמה. אם אני אומר 'אני גבוה', זה נכון או שקר. אם אני אומר, 'אתה גבוה', זה נכון או שקר. אם אני גבוה ואתה נמוך, ונשאלת השאלה אם גם אתה וגם אני גבוהים, בלוגיקה בוליאנית, יש לתת תשובה של נכון או לא נכון. איזה משני אלה צריך לתת? בול לא באמת ענה על השאלה הזו. הוא פשוט המציא מערכת של כללים שנפעל לפיהם. החדשות הטובות הן שכשאתה פועל לפי הכללים האלה בהקשר הנכון שלהם, אין לך אי בהירות. הודות לכללים הללו, יש לנו היום מחשבים ותכנות. הכללים ניתנים לך עכשיו. לא באמת ניתן להסביר את הכללים; אתה פשוט מקבל אותם. הכללים נמצאים תחת שלוש כותרות: AND, OR ו- NOT.
ו
אפשר לשאול את השאלה אם גם אתה וגם אני גבוהים. הגובה שלי והגובה שלך משולבים אז על ידי מערכת הכללים AND. אלו הם הכללים AND שיש לפעול לפיהם:
false AND false = false
false AND true = false
true AND false = לא נכון
נכון ואמת = נכון
עכשיו, תן לגובה להיות נכון ולקצר להיות שקר. זה אומר שאם אני נמוך ואתה נמוך, אתה ואני נמוכים. אם אני נמוך ואתה גבוה, אתה ואני נמוכים; זו התשובה הבוליאנית שאתה צריך לקבל. אם אני גבוה ואתה נמוך, גם אתה וגם אני נמוכים. אם אני גבוה ואתה גבוה, אתה ואני גבוהים. כל אלה הם חוקים בוליאניים שאתה (הקורא) רק צריך לקבל.
אוֹ
ניתן לשאול את השאלה אם אתה או אני גבוה. הגובה שלי והגובה שלך משולבים אז על ידי מערכת הכללים OR. אלו הם כללי ה-OR שיש לפעול לפיהם:
false OR false = false
false OR true = true
true OR false = נכון
true OR true = true
שוב, תן לגובה להיות נכון ולקצר להיות שקר. זה אומר שאם אני נמוך או שאתה נמוך, אתה או אני נמוך. אם אני נמוך או שאתה גבוה, אתה או אני גבוהים. אם אני גבוה או שאתה נמוך, אתה או אני גבוה. אם אני גבוה או שאתה גבוה, אתה או אני גבוהים. כל אלה הם כללים בוליאניים שאתה צריך לקבל.
לֹא
כעת, בלוגיקה הבוליאנית, קיימים רק שני מצבים (תשובות אפשריות). כלומר, אם אתה לא גבוה, אתה נמוך. אם אתה לא נמוך, אתה גבוה; שום דבר אחר. אלו הם כללי ה- NOT שיש לפעול לפיהם:
לא שקר = נכון
לא נכון = לא נכון
נניח שיש לך חוט (או קפיץ) שאתה יכול להאריך (למשוך). בעוד המחרוזת במצבו הטבעי, אם אני אומר, 'לא קצר', היית מאריך אותו; זו הפרשנות. בזמן שהמחרוזת מורחבת, אם אני אומר 'לא ארוך', היית מאפשר לה להתכווץ; זו הפרשנות.
אתה צריך לשנן את כל הכללים הנתונים בקטגוריות השונות שלהם.
יותר משני אופרנדים
בשפת מחשב, AND, OR ו- NOT נקראים כל אחד אופרטור. עבור האופרטור NOT, אתה צריך רק אופרנד אחד (ערך לאופרטור) כדי לקבל תשובה. עבור האופרטורים AND או OR, אתה יכול לקבל יותר משני אופרנדים. המקרים הקודמים מציגים שני אופרנדים עבור AND ו-OR. אתה יכול לקבל שלושה אופרנדים עבור AND באופן הבא:
false AND false AND false = שקר
false AND false AND true = false
אלו שני קווים; לכל אחד יש שני אופרטורים AND. יש למעשה תשע שורות כאשר האופרנדים הם שלושה. עם האופרטור AND, רק השורה האחרונה (השורה התשיעית) שווה ל-true; כל השורות הקודמות שקר. שים לב שעם שני אופרנדים עבור AND, רק השורה האחרונה עדיין נכונה; כל שלוש השורות הקודמות שגויות. כאשר האופרנדים הם ארבעה, יש 16 שורות ורק השורה האחרונה נכונה לאופרטור AND.
הדפוס עבור AND והדפוס עבור OR שונים. עם שלושה אופרנדים לשני אופרטורים OR, יש גם תשע שורות ורק השורה הראשונה, הפעם, היא שקר. השורה השנייה עד התשיעית נכונה. שים לב שעם שני אופרנדים עבור OR, רק השורה הראשונה עדיין נכונה; כל שלושת השורות הנותרות הן שקר. כאשר האופרנדים הם ארבעה עבור OR, יש גם 16 שורות.
האופרטור NOT עוסק באופרנד אחד בלבד. ה-not false הוא נכון וה- NOT true הוא שקר.
2.2 שני טבלת אמת אופרנד והרכיבים האלקטרוניים שלהם
במתמטיקה ישנו נושא שנקרא אלגברה. חלק קטן ממנו נראה בפרק הקודם. יש סוג של אלגברה שנקראת אלגברה בוליאנית. באלגברה בוליאנית, אמת מזוהה על ידי ספרת בסיס שתיים שהיא 1 ו-false מזוהה על ידי ספרת בסיס שתי שהיא 0.
רכיבי יחידת המחשב הפנימיים הם רכיבים אלקטרוניים. יחידת המערכת של מערכת המחשוב כוללת רכיבים אלקטרוניים דיגיטליים. פעולת ה-AND נעשית על ידי רכיב אלקטרוני קטן הנקרא שער AND. פעולת ה-OR נעשית על ידי הרכיב האלקטרוני הקטן הנקרא שער OR. פעולת NOT מתבצעת על ידי הרכיב האלקטרוני הקטן הנקרא NOT gate. יותר מדי מהשערים הללו יכולים להיות בשבב מעגל משולב (IC).
ושולחן האמת והשער שלו
הטבלה הבאה נותנת את טבלת האמת AND ואת הסמל שלה שער AND (מעגל קטן):
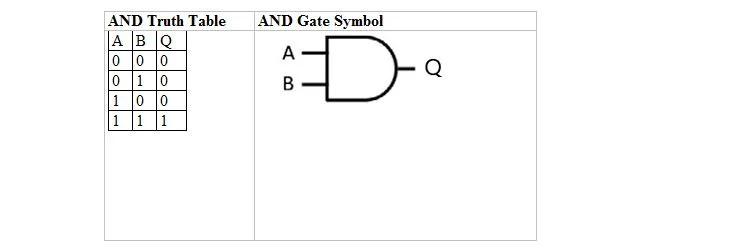
הן עבור טבלת האמת AND והן עבור השער שלה, A כמו גם B הם שני משתני קלט. Q הוא משתנה הפלט. A הוא 1 או 0. B הוא 1 או 0. Q הוא 1 או 0. טבלת האמת AND עם 1 ו-0 זהה לפריסת האמת/לא נכון והאמת הקודמת (טבלה). משוואת AND היא:
א . B = Q
כאשר הנקודה (.) פירושה AND (בוליאנית). ניתן להשמיט את הנקודה כדי לקבל AB = Q שפירושו אותו דבר (AND).
הערה: הביטים עבור A ו-B בארבע השורות, כזוגות, הם ארבעת המספרים הראשונים בבסיס שני המתחילים מ-0 (או 00), כלומר 00, 01, 10, 11.
הטבלה הבאה נותנת את טבלת האמת OR ואת סמל שער ה-OR (מעגל קטן) שלה:
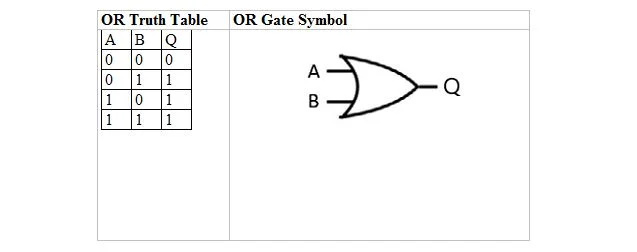
הן עבור טבלת האמת OR והן עבור השער שלה, A כמו גם B הם שני משתני קלט. Q הוא משתנה הפלט. טבלת האמת של OR עם 1 ו-0 זהה לפריסת האמת הקודמת/לא נכון OR (טבלה).
משוואת ה-OR היא:
A + B = Q
כאשר ה-+ כאן פירושו בוליאני OR ולא חיבור. המשוואה נקראת 'A או B שווה ל-Q'.
הטבלה הבאה נותנת את טבלת האמת NOT ואת סמל השער NOT (מעגל קטן) שלה:
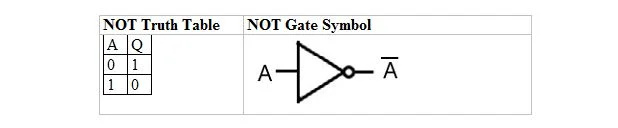
לטבלת האמת NOT או שער NOT יש רק קלט אחד ופלט אחד. כאשר הקלט הוא 0, הפלט הוא 1. כאשר הקלט הוא 1, הפלט הוא 0. שער NOT עושה סוג של היפוך. משתנה הפלט זהה למשתנה הקלט, אבל עם סרגל (שורה מעל). טבלת האמת NOT עם 1 ו-0 זהה לפריסת האמת/לא נכון או האמת הקודמת (טבלה).
משוואת ה- NOT היא:
א = ש
כאשר Q = A והסרגל מעל A כאן פירושו השלמה. המשלים של 0 הוא 1 והמשלים של 1 הוא 0. השער NOT ידוע גם בתור ה-INVERTING gate.
אלו הן טבלאות האמת הבסיסיות (או השורשיות) והשערים שלהן (מעגלים קטנים) באלקטרוניקה דיגיטלית (עם אלגברה בוליאנית). שלושת טבלאות האמת האחרות המובאות באיור הבא והשערים שלהן מיועדות לנוחות ומבוססות על שלושת טבלאות האמת הקודמות.
יש טבלת אמת ושער שנגזרים מטבלת ושער האמת AND. הם נקראים טבלת האמת NAND (עבור NOT AND) ושער ה-NAND המתאים. טבלת האמת NAND ושער ה-NAND שלה הם:
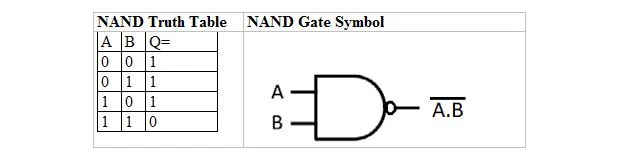
כדי לקבל את טבלת האמת NAND, עבור אל הפלט של טבלת האמת AND והחלף כל ספרה בהשלמה שלה. המשלים של 0 הוא 1 והמשלים של 1 הוא 0. שער ה-NAND הוא כמו שער ה-AND, אבל יש לו עיגול קטן לפני קו המוצא. משוואת NAND היא:
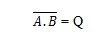
איפה פירושו השלמה של התוצאה של 'A' ו-'B'. הבר (קו-על) מיוצג בשער על ידי העיגול הקטן. שימו לב שניתן להשמיט את הנקודה בין A ל-B.
יש עוד טבלת אמת ושער שנגזרים מטבלת האמת והשער של OR. הם נקראים טבלת האמת NOR (עבור NOT OR) ושער NOR המתאים. טבלת האמת NOR ושער NOR שלו הם:
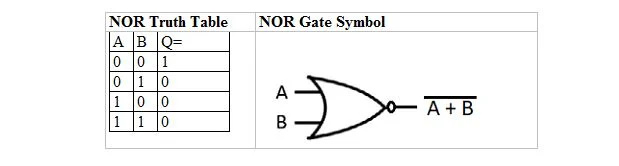
כדי לקבל את טבלת האמת NOR, עבור אל הפלט של טבלת האמת OR והחלף כל ספרה בהשלמה שלה. המשלים של 0 הוא 1 והמשלים של 1 הוא 0. שער NOR הוא כמו שער OR, אבל יש לו עיגול קטן לפני קו המוצא. משוואת NOR היא:
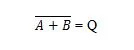
איפה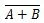 
פירושו השלמה של התוצאה של 'A' או 'B'. הבר (קו-על) מיוצג בשער על ידי העיגול הקטן.
בלעדי OR (XOR)
טבלת האמת עבור שער ה-OR היא:
באנגלית רגילה, לא ברור אם השורה האחרונה של 1 או 1 צריכה לתת 1 או 0. אז, באלגברה בוליאנית, ישנם שני סוגים של טבלאות אמת OR ושני שערים תואמים. עם ה-OR הרגיל, השורה האחרונה של 1 או 1 נותנת 1. הסוג השני של OR הוא האקסקלוסיבי-OR (XOR) שבו שלוש השורות הראשונות זהות לשלוש השורות הראשונות של OR רגיל (כולל פלט). עם זאת, עבור השורה הרביעית והאחרונה, 1 או 1 נותן 0.
הטבלה הבאה נותנת את טבלת האמת XOR ואת סמל השער XOR (מעגל קטן) שלה:
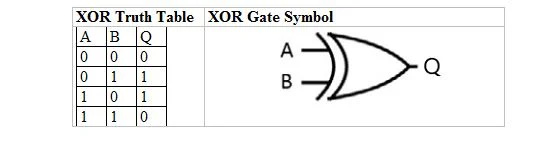
הן עבור טבלת האמת XOR והן עבור השער שלה, 'A' וכן 'B' הם שני משתני קלט. 'Q' הוא משתנה הפלט.
משוואת XOR היא:
A ⊕ B = Q
כאשר ⊕ כאן פירושו XOR בוליאני.
ה-OR הרגיל פירושו אחד או שניהם. בלעדי OR פירושו בהחלט אוֹ ולא שניהם.
2.3 פוסטולציות בוליאניות
הנחות הן הנחות המבוססות על מסקנות מסוימות. ישנן עשר פוסטולציות בוליאניות שמקורן במשוואות AND, OR ו- NOT (טבלאות אמת). משוואות אלו נקראות גם פונקציות. הפונקציות הבסיסיות מועתקות באופן הבא:
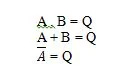
אלו הן הפונקציות הבסיסיות (משוואות) באלגברה בוליאנית. שלושת המשוואות האחרות הבאות (פונקציות) אינן פונקציות בסיסיות:
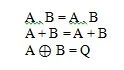
למרות שהפונקציה האחרונה כאן היא מוזרה, היא לא נחשבת כפונקציה בסיסית.
ההנחות הבוליאניות הן כדלקמן:
מ-AND Function
1) 0 . 0 = 0
עשרים . 1 = 0
3) 1. 0 = 0
4) 1. 1 = 1
מפונקציית OR
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1
מתוך NOT Function
9) 0 = 1
10) 1 = 0
הערה: ההנחות הללו הן רק השורות בטבלאות AND, OR, ו-NO האמת שבאות לידי ביטוי באופן עצמאי. על הקורא לשנן את ההנחות הנתונות.
2.4 מאפיינים בוליאניים
נכס הוא מאפיין דומה למשהו. תכונות בוליאניות הן משוואות שנגזרות מההנחות הבוליאניות. בסעיף זה, המאפיינים ניתנים פשוט ללא גזירותיהם ולאחר מכן נעשה בהם שימוש. ישנם עשרים וחמישה מהנכסים המקובצים תחת עשר כותרות כדלקמן:
מאפיינים של הפונקציה AND
נכס 1:
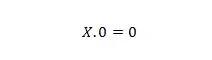
כאשר X יכול להיות 1 או 0. זה אומר שלא משנה מהו X, התוצאה היא תמיד 0.
הערה: משתנה לא חייב להיות בהכרח A או B או C או D. משתנה יכול להיות W או X או Y או Z או כל אות אחרת.
נכס 2:
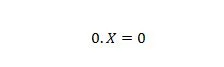
כאשר X יכול להיות 1 או 0. שימו לב שההבדל בין תכונה 1 לתכונה 2 הוא שבצד שמאל של סימן השוויון של שתי המשוואות, המיקומים של X ו-0 מתחלפים.
נכס 3:
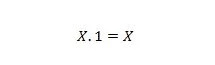
אם X הוא 0, אז 0. 1 = 0. אם X הוא 1, אז 1. 1 = 1.
נכס 4:
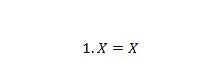
אם X הוא 0, אז 1. 0 = 0. אם X הוא 1, אז 1. 1 = 1. שימו לב שההבדל בין תכונה 3 לתכונה 4 הוא שבצד שמאל של שתי המשוואות, המיקומים של X ו-1 מתחלפים.
מאפיינים של פונקציית ה-OR
נכס 5:
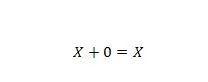
כאשר X יכול להיות 1 או 0. זה אומר שאם X הוא 0, התוצאה היא 0. אם X הוא 1, התוצאה היא 1.
נכס 6:
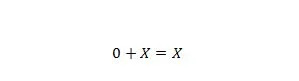
כאשר X יכול להיות 1 או 0. שימו לב שההבדל בין תכונה 5 לתכונה 6 הוא שבצד שמאל של שתי המשוואות, המיקומים של X ו-0 מתחלפים.
נכס 7:
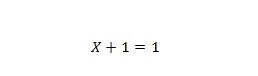
אם X הוא 0, אז 0 + 1 = 1. אם X הוא 1, אז 1 + 1 = 1.
נכס 8:
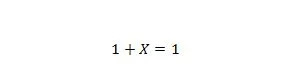
אם X הוא 0, אז 1 + 0 = 1. אם X הוא 1, אז 1 + 1 = 1. שימו לב שההבדל בין תכונה 7 לתכונה 8 הוא שבצד שמאל של שתי המשוואות, המיקומים של X ו-1 מתחלפים.
מאפיינים הנוגעים לשילוב של משתנה עם עצמו או משלו
נכס 9: 
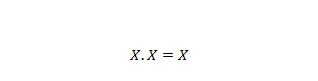
כלומר: אם X הוא 0, אז 0 . 0 = 0. אם X הוא 1, אז 1. 1 = 1.
נכס 10:
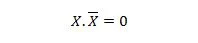
כלומר: אם X הוא 0, אז 0. 1 = 0. אם X הוא 1, אז 1. 0 = 0.
עבור משתנים עוקבים, מאפיין זה הופך ל:
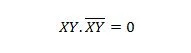
נכס 11:
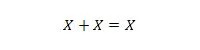
כלומר: אם X הוא 0, אז 0 + 0 = 0. אם X הוא 1, אז 1 + 1 = 1 (מ-OR רגיל).
נכס 12:
כלומר: אם X הוא 0, אז 0 + 1 = 1. אם X = 1, אז 1 + 0 = 1.
כלומר: אם X הוא 0, אז 0 + 1 = 1. אם X = 1, אז 1 + 0 = 1.
השלמה כפולה
נכס 13:
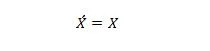
כאשר X בצד שמאל הוא 0, X בצד ימין הופך ל-0. כאשר X בצד ימין הוא 1, X בצד שמאל הופך ל-1. במילים אחרות, השלמות כפולות מחזירות את הערך המקורי.
חוק חלופי
נכס 14:
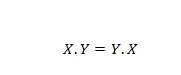
המשמעות היא שהחלפת האופרנד הראשון והשני עבור האופרטור AND, בצד שמאל של סימן השוויון, לא משנה; התשובה עדיין זהה לאחר שההחלפה בצד שמאל התבצעה. ניתן לכתוב משוואה זו כאשר הנקודות מושמטות כך: XY = YX.
נכס 15:
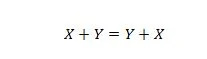
ההסבר כאן זהה ל-AND הקודם, אבל הוא מיועד לאופרטור OR.
חוק חלוקתי
נכס 16:
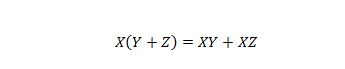
כאן ישנם שלושה משתנים: X, Y ו-Z. כל משתנה יכול להיות 1 או 0. בצד שמאל של הסמל השווה, משמעות הסוגריים היא להעריך קודם כל מה יש בהם. ואז, AND היא התוצאה עם X. הצד הימני אומר שה-X ו-Y יחד, או ה-X ו-Z יחד, זהים לצד השמאלי. שימו לב שאופרטור הנקודה עבור ה-AND מושמט לכל אורכו; והמשתנים המצורפים עדיין פירושם AND.
נכס 17:
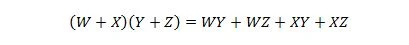
מאפיין זה הוא הרחבה של מאפיין 16 בתוספת המשתנה של W.
משפט אסוציאטיבי
נכס 18:
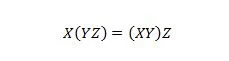
משמעות הסוגריים היא להעריך תחילה מה יש בסוגריים. לכן, עבור הביטוי בצד שמאל, אם Y עם Z מסומנים ראשון ב-AND, ו-X מסומן ב-AND עם התוצאה, אז התוצאה הסופית בצד שמאל זהה לתוצאה הסופית בצד ימין -יד-side כאשר X עם Y הוא ANDed ראשון לפני ANDing התוצאה עם Z. שימו לב שהנקודות הושמטו במשוואה.
נכס 19:
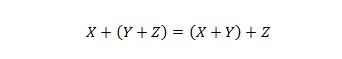
מאפיין זה מוסבר בצורה דומה למאפיין 18, אך האופרטור OR מועסק במקום האופרטור AND. האופרטור OR + לעולם אינו מושמט מביטוי בוליאני לשם הפשטות. מצד שני, ניתן להשמיט את האופרטור AND ולחבר את שני המשתנים.
קְלִיטָה
נכס 20:
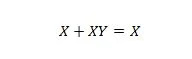
עם המשוואה הזו, לא משנה מהו Y, הצד הימני תמיד יהיה X (נספג).
נכס 21:
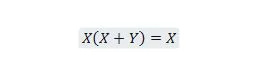
כמו כן, עם המשוואה הזו, לא משנה מהו Y, הצד הימני תמיד יהיה X (נספג). מאפיין זה 21 זהה למאפיין 20 שהוא:
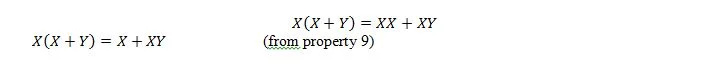
כאן אנו משתמשים בחוק החלוקתי ובעובדה ש-X.X = X של מאפיין 9.
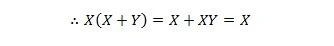
זהות
נכס 22:
המשמעות היא שעבור הביטוי X + Y, ההשלמה של X מול Y לא משנה את הביטוי.
נכס 23:
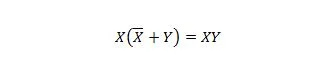
המשמעות היא שעבור ביטוי XY, ההשלמה של X ORed עם Y בסוגריים, שנעשה תחילה, לא משנה את ביטוי XY.
חוק דמורגן
נכס 24:
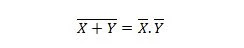
המשמעות היא שלשער NOR (NOT OR) יש את אותה תוצאה כמו ציון שתי הכניסות לפני AND אותם.
נכס 25:
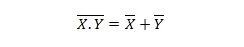
המשמעות היא שלשער NAND (NOT AND) יש את אותה תוצאה כמו ציון שתי הכניסות לפני ORing.
האיורים המסופקים הם 25 הנכסים. ניתן להוכיח אותם על ידי החלפת כל הערכים האפשריים השונים של 1 ו-0, בכל ביטוי בצד שמאל, כדי לראות אם הביטוי (או התוצאה) בצד ימין מתקבל. ההוכחות נשארות כתרגיל לקורא.
2.5 פישוט של ביטויים מורכבים
שתי הפונקציות הבאות זהות:
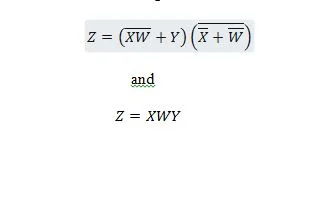
Z הוא הפלט ו-X, W ו-Y הם הכניסות. הראשון צריך שער NAND, שער OR, שער AND, שני שערים NOT, שער OR ושער NOR. השני צריך רק שני שערים ו-AND. הראשון הוא משוואה עם ביטוי מורכב, בצד ימין, שפושטה (הצטמצמה) למונח הביטוי הימני היחיד עבור המשוואה השנייה.
פישוט או הפחתה מובילים למספר קטן יותר של שערים על מנת ליישם את אותה פונקציה כמו מעגל. מעגל קטן כזה יכול להיות חלק ממעגל משולב (IC) או להיות מעגל עצמאי על פני לוח האם של המחשב.
כאשר פונקציה (משוואה) מגיעה לתהליך התכנון, יש לבצע פישוט כדי לצמצם את מספר השערים ולסיים עם מעגל זול יותר. לפישוט צריך להשתמש באחד או יותר מעשרים וחמישה המאפיינים הבוליאניים הקודמים.
דוגמה 2.51:
הקטינו את המשוואה:
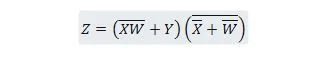
הערה: שני סוגריים אחד ליד השני פירושם שהסוגריים הם ANDed (הנקודה ביניהם לא נכתבה באופן אופציונלי).
פִּתָרוֹן:
לפתרונות, ההצדקה (הסיבה) לכל צעד ניתנת בצד ימין של המדרגה, בסוגריים. על הקורא לקרוא כל שלב והצדקתו. הקורא צריך גם להתייחס למאפיינים הקודמים בזמן שהוא/היא קורא את שלבי הפחתת הפונקציות.
דוגמה 2.52:
לפשט:
2.6 סכום מינימלי של מוצרים
שתי הפונקציות הבאות זהות:
שני הביטויים הימניים של שתי המשוואות אמורים להיות בצורת סכום המוצרים (SP). אומרים שביטוי מפורש הוא בצורת סכום המוצר אם אין לו סוגריים. ברור שהפונקציה הראשונה (המשוואה) צריכה יותר שערים מהפונקציה השנייה.
עדיין ניתן לצמצם את הביטוי הימני הראשון כדי להשיג את הפונקציה השנייה. לא ניתן לפשט את הביטוי השני בצד ימין ועדיין להתבטא כסכום מוצרים ('תוספת' של מונחים). את הביטוי הימני השני אי אפשר באמת לפשט עוד יותר. אז, אומרים שהוא בצורת מינימום סכום מוצרים (MSP).
דוגמה 2.61:
הביאו את הפונקציה הבאה תחילה לטופס סכום המוצרים ולאחר מכן לטופס מינימום סכום מוצרים.
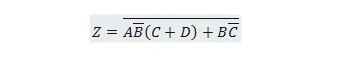
פִּתָרוֹן:
בעת פתרון בעיות כמו זה, יש להשתמש באחד או יותר מעשרים וחמש המאפיינים הקודמים כפי שמוצג בפתרון זה:
2.6 סכום מינימלי של מוצרים
שתי הפונקציות הבאות זהות:
שני הביטויים הימניים של שתי המשוואות אמורים להיות בצורת סכום המוצרים (SP). אומרים שביטוי מפורש הוא בצורת סכום המוצר אם אין לו סוגריים. ברור שהפונקציה הראשונה (המשוואה) צריכה יותר שערים מהפונקציה השנייה.
עדיין ניתן לצמצם את הביטוי הימני הראשון כדי להשיג את הפונקציה השנייה. לא ניתן לפשט עוד יותר את הביטוי הימני השני ועדיין להתבטא כסכום מוצרים ('הוספה' של מונחים). אי אפשר באמת לפשט יותר את הביטוי הימני השני. אז, אומרים שהוא בצורת מינימום סכום מוצרים (MSP).
דוגמה 2.61:
הביאו את הפונקציה הבאה תחילה לטופס סכום המוצרים ולאחר מכן לטופס מינימום סכום מוצרים.
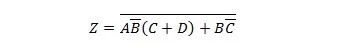
פִּתָרוֹן:
בעת פתרון בעיות כמו זה, יש להשתמש באחד או יותר מעשרים וחמש המאפיינים הקודמים כפי שמוצג בפתרון זה:
ביטוי אחרון זה הוא בצורת סכום המוצרים (SP), אך לא בצורה של מינימום סכום מוצרים (MSP). החלק הראשון של השאלה נענה. הפתרון לחלק השני הוא כדלקמן:
הפונקציה המפושטת האחרונה הזו (המשוואה) היא בצורת MSP, וצריכה פחות מספר שערים ליישום מאשר צורת ה-SP המקבילה לה. זכור: SP פירושו סכום מוצרים ואילו MSP פירושו סכום מינימום של מוצרים.
דוגמה 2.62:
למעגל הבא יש כניסות X, Y ו-W ו-Z הוא הפלט. הפק את פונקציית סכום המוצרים (SP) (הסכום המינימלי לכאורה של פונקציית המוצרים) עבור Z. לאחר מכן, הפק את הסכום האמיתי יותר (מוזער) של סכום המוצרים (MSP). לאחר מכן, יישם את מעגל MSP (צייר את רשת ה-Gating MSP).
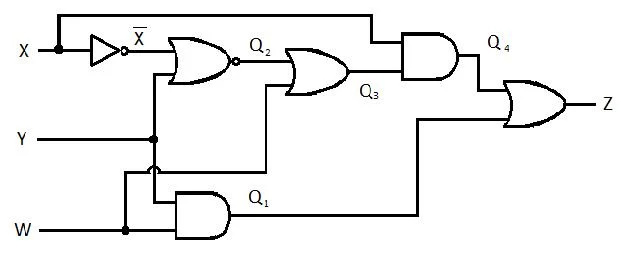
איור 2.61 A Circuit Gate
פִּתָרוֹן:
לפני שתהליך הפישוט מתחיל, יש לקבל את הביטוי של Z במונחים של X, Y ו-W. עיין באיור לדוגמה זה מהתרשים:
זהו הביטוי של Z במונחים של X, Y ו-W. לאחר מכן, הפשטה ל-MSP לכאורה יכולה להתרחש. לכאורה MSP הוא SP.
המשוואה (הפונקציה) האחרונה הזו היא בצורת SP. זה לא נכון סכום מינימום של מוצרים (עדיין לא MSP). אז, צמצום (מזעור) צריך להמשיך.
המשוואה האחרונה (פונקציה) היא סכום מינימום אמיתי של מוצרים (MSP). ומעגל השער המינימלי של מוצרים (מזעור אמיתי) הוא:
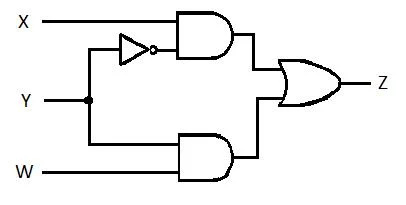
איור 2.62 MSP Gating Circuit
תגובה
מהניתוח בסעיף זה ניתן לראות כי לא ברור אם סכום המוצרים הוא סכום המינימום של מוצרים או לא. SP לא מאוד שימושי. זה MSP שהוא מאוד שימושי. יש דרך בטוחה להשיג MSP; זה להשתמש במפת Karnaugh. מפת Karnaugh היא מעבר להיקף של קורס קריירה מקוון זה.
2.7 בעיות
מומלץ לקורא לפתור את כל הבעיות בפרק לפני המעבר לפרק הבא.
- הפק את טבלאות האמת AND, OR ו- NOT עם השערים המתאימים להם.
- רשום את עשר ההנחות הבוליאניות בקטגוריות השונות שלהן, ותן שם לקטגוריות.
- ללא הסבר, רשום את עשרים ושש המאפיינים של האלגברה הבוליאנית בקטגוריות השונות שלהן, ותן שם לקטגוריות.
- צמצם את המשוואה באמצעות המאפיינים הבוליאניים וציטוט הקטגוריות בהן נעשה שימוש.
- צמצם את המשוואה באמצעות המאפיינים הבוליאניים וציטוט הקטגוריות בהן נעשה שימוש.
- באמצעות המאפיינים הבוליאניים וציטוט הקטגוריות בהן נעשה שימוש, צמצם את המשוואה הבאה - תחילה לסכום מוצרים ולאחר מכן לסכום מינימלי של מוצרים:
- באמצעות המאפיינים הבוליאניים וציטוט הקטגוריות בהן נעשה שימוש, צמצם את המשוואה הבאה - תחילה לסכום מוצרים ולאחר מכן לסכום מינימלי של מוצרים:
