פרק 3: פעולות מספר בינארי במיקרו-מעבד
3.1 מבוא
במחשב, פעולות אריתמטיות נעשות ב-8 סיביות, 16 סיביות, 32 סיביות או 64 סיביות. מספר כמו 3 בבינארי הוא 11. אם הפעולה אמורה להתבצע ב-8 סיביות, זה נחשב כ-00000011; לפניה 0 אפסים.
עבור מספר בינארי כמו 10000101, הביט המשמעותי ביותר הוא הביט בצד שמאל קיצוני. זה 1 במקרה הזה. הביט הפחות משמעותי הוא הביט הקיצוני מימין, שהוא עדיין 1, עבור המספר. החלק המשמעותי ביותר מקוצר כ-MSB. החלק הפחות משמעותי מקוצר LSB.
הספרה הבינארית מקוצרת כ-BIT ונכתבת בפשטות כ-bit. במספר 10010011, כל אחד או אפס זה קצת. קבוצה של ארבע ביטים נקראת ניבול. קבוצה של שמונה ביטים נקראת בייט. בייט מורכב משני נישנושים. הנשנוש התחתון הוא הנשנוש עבור ה-LSB והנשנש הגבוה יותר הוא הנשנוש עבור ה-MSB.
קבוצה של 8 סיביות, 16 סיביות, 32 סיביות או 64 סיביות נקראת מילה, כל עוד קבוצה זו מעבירה מידע מעבר לציון מספר בלבד. הקבוצה נקראת מילה, למשל, אם מדובר בהוראה ברמה נמוכה במחשב. יש גם מילה של 24 סיביות, אבל זה לא נפוץ היום.
Endianness מתייחס לסדר שבו הבתים יוצרים מילה. שקול את המילה 24 סיביות - 100100001111010100100010. מילה זו מורכבת משלושה בתים שהם:
10010000 11110101 00100010
הבית המשמעותי ביותר הוא הבית השמאלי ביותר. כאשר ה-byte בצד שמאל הקיצוני הוא הבית המשמעותי ביותר וה-byte בצד ימין הקיצוני הוא הבית הפחות משמעותי, זה מכונה ייצוג Big Endian של המילה. הייצוג הקטן אנדיאן הוא הפוך.
זיכרון המחשב הוא סדרה של תאים, וכל תא מכיל בתים. התא הראשון בזיכרון המחשב מיועד לבייט 0, השני מיועד לבייט 1, השלישי הוא עבור בייט 2, וכן הלאה. עם אנדיאניות גדולה ועבור המילה הקודמת, הבית המשמעותי ביותר מאוחסן בתא בייט 0, הבית האמצעי מאוחסן בתא בייט 1, והבייט הכי פחות משמעותי מאוחסן בתא בייט 2. המשמעות היא שיש בתים משמעותיים יותר בתא הזיכרון התחתון.
ניתן לכתוב את המילה הקודמת של 24 סיביות בסדר הפוך של בתים באופן הבא:
00100010 11110101 10010000
כעת, הבית הכי פחות משמעותי נמצא בשמאל הקיצוני והבייט המשמעותי ביותר נמצא בימין הקיצוני. כאשר ה-byte בצד שמאל הקיצוני הוא ה-byte הכי פחות משמעותי וה-byte בצד ימין הקיצוני הוא ה-byte המשמעותי ביותר, זה הייצוג Little Endian של המילה. עם מעט קצה ועבור המילה הקודמת, הבית הכי פחות משמעותי מאוחסן בתא בייט 0, הבית האמצעי מאוחסן בתא בייט 1, והבייט המשמעותי ביותר מאוחסן בתא בייט 2. משמעות הדבר היא שיש בתים פחות משמעותיים בתא הזיכרון התחתון.
Endianness לא משמש עבור ביטים בבייט. זה גם לא משמש לנשנושים בבייט. הוא משמש רק לסדר בתים.
שורת המספרים
מספר ללא סימן הוא מספר חיובי. מספרים חיוביים הם מספרים מאפס העולים כלפי מעלה. קיימים גם מספרים שליליים. ניתן להציג מספרים חיוביים ושליליים על קו מספרים. קו המספרים הבא מציג את המספרים השלמים החיוביים והשליליים (שלמים) ליד אפס:
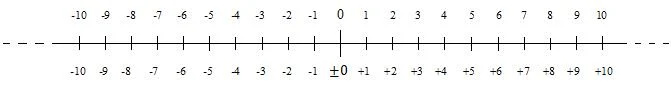
מספרים שליליים יורדים מאפס כלפי מטה (שמאלה). במצבים רבים, אפס נחשב כחיובי. עם זאת, זה נחשב לשלילי במצבים מסוימים. לכן יש סימן פלוס ומינוס לפני אפס, במספור התחתון, בתרשים. כאשר מספר חיובי, ניתן להשמיט את הסימן שלו; זה המקרה עבור המספור העליון בתרשים. סימן המינוס מול מספר שלילי לעולם אינו מושמט.
3.2 חיבור של מספרים בינאריים
בתוספת:
A + B = S
A נקרא אוגד, B נקרא תוספת, ו-S נקרא סכום.
שקול את החיבור הבא של שני מספרים חיוביים בבסיס שני:

בבסיס שני, הספרות האפשריות היחידות הן 0 ו-1. חיבור בבסיס 2 דומה לחיבור בבסיס עשר, אבל שתיים בבסיס שתיים היא אחת-אפס (10). כאשר הסכום של שני ביטים בעמודה הוא 10, נכתב 0 ו-1 מועבר לעמודה השמאלית המיידית; יש להוסיף לסכום של שני הביטים שם. כאשר הסכום הכולל הוא שלושה, זה אומר 11 בבסיס שני. ה-1 ל-11 הימני נכתב וה-1 השמאלי נישא כדי להתווסף לסכום סיביות העמודה השמאלית המיידית. בכל מקרה, ה-1 הנישא שמאלה נקרא נשיאה.
קריאת טבלת ההוספות הקודמת מימין, בעמודה השנייה (מימין), ישנה סחיבה הנובעת מ-1+1 = 10. בעמודה השלישית, ישנה סחיבה הנובעת מ-1+1+ נשיאה של 1 = 11. בעמודה הרביעית, יש נשיאה הנובעת מ-0+1+ נשיאה של 1 = 10. בעמודה החמישית, אין נשיאה מכיוון שהסיכום הוא 0+0+ נשיאה של 1 = 1. שאר העמודות אינו כרוך בהובלה.
ספירת העמודות מתחילה מהקצה הימני. עם תוספת של 16 סיביות, יכול להיות העברה מהעמודה השמינית לעמודה התשיעית (נע שמאלה). הטבלה הבאה ממחישה זאת:

פעולות אריתמטיות ולוגיות מתרחשות במיקרו-מעבד בלוח האם של המחשב.
עבור מחשב מילים של 8 סיביות, ה-carry לא יכול לעבור מהביט השמיני לסיביות התשיעית באופן אוטומטי על ידי חומרה. לכן, כדי להוסיף שתי קבוצות של 16 סיביות במחשב כזה, התוספת צריכה להיעשות פעמיים בשמונה-שמונה סיביות זוגות. ההובלה מועברת ומתבצעת על ידי התוכנה (תכנות).
כדי להוסיף שני מספרים, ניתן להמיר את המספרים תחילה לצורת ההשלמה של השניים שלהם (ראה להלן) לפני ההוספה.
3.3 משלים של שניים וחיסור המספרים הבינאריים שלו
בלוח האם של המחשב, יש את הזיכרון ויש את המיקרו-מעבד ומעגלים אחרים. הזיכרון הוא סדרה של תאים של שמונה סיביות. עבור בייט, כל סיביות נכנסות לתא. למיקרו-מעבד יש כמה מיקומים מסוג זיכרון. מיקומים מסוג זיכרון אלה נקראים אוגרים. לכן, במחשב, ניתן לאחסן קבוצות של בתים באופן זמני בזיכרון או באוגרים של המיקרו-מעבד.
בכל אחד מהמחסנים האלה, כל תא יכול לקבל 1 או 0, ולא שום דבר אחר. בחיים יש מספרים חיוביים ושליליים. מספר חיובי מתחיל בסימן פלוס (+) ומספר שלילי מתחיל בסימן שלילי (-). כאשר הסימן מושמט, המספר נחשב כמספר חיובי.
על מנת לפתור בעיה זו של ציון סימן מספר במחשב, נשמרים המספרים השלמים בטווחים. מספרים שלמים הם מספרים שלמים. אם משתמשים בשמונה סיביות לאחסון טווח המספרים האפשריים, הסיבית השמאלית ביותר משמשת כסיבית הסימן. אם המספר מתחיל ב-0, המספר הוא מספר חיובי. אם הוא מתחיל ב-1, המספר הוא מספר שלילי. אם משתמשים בשש עשרה סיביות לאחסון טווח המספרים האפשריים, הסיבית השמאלית ביותר משמשת כסיבית הסימן. אם המספר מתחיל ב-0, t המספר הוא מספר חיובי. אם הוא מתחיל ב-1, המספר הוא מספר שלילי. המספרים בטופס זה נקראים מספרים חתומים.
בפועל, יכולים להיות מספרים חתומים עבור 8 סיביות, 16 סיביות, 32 סיביות ו-64 סיביות. ככל שמשתמשים במספר סיביות רחב יותר, כך גדל טווח המספרים האפשריים שניתן לאחסן.
מספרים שלמים משלימים של שני
עם ההשלמה של שניים, המספרים החיוביים הם המספרים הרגילים הספירה, אלא שהספרה השמאלית ביותר היא 0. כדי לקבל את המספר השלילי המתאים לכל מספר חיובי נתון, הפוך כל סיביות במספר והוסף 1 לתוצאה. ההיפוך או המשלים של 0 הוא 1. ההיפוך או המשלים של 1 הוא 0. הטבלאות הבאות מציגות מספרים משלימים של כמה שניים בטווחים שלהם:
| טבלה 3.31 מספרים שלמים משלימים בשני ביטים |
|
|---|---|
| בינארי | נקודה |
| 01 | +1 |
| 00 | +0 |
| אחד עשר | -1 |
| 10 | -2 |
המספרים הבינאריים החיוביים הם 00 ו-01 (כלומר אפס ואחד). בחלק השמאלי ביותר, אפס מראה שהם מספרים חיוביים. 00 הוא קצת באמצע הטווח. כדי לקבל -1, ההיפוך של המספר 01 נמצא 10. הוספת 1 לזה (בקצה הימני) נותן 11.
מכיוון שמשתמשים בשתי סיביות, נותר רק סיביות אחת לייצג את המספרים בטווח המורכב מהמספרים +1, +0 ו-1 המתאימים ל-01, 00 ו-11. הסיביות הראשונה מציינת את הסימן. קורה ש-10 עבור +2 אינו בין שלושת המספרים הבינאריים הללו. 10 מתחיל ב-1 כלומר עליו להיות מספר שלילי בהשלמה של שניים. אז, 10 נכלל בטווח, כלומר -2.
עם שני ביטים בהשלמה של שניים, המספר של כל המספרים השלמים (חיוביים ושליליים) שניתן לייצג הוא 2 2 = 4 ולא 2 2 -1 = 3. הניואנס נובע מהכללת המספר השלילי האחרון שהוא השלילי של 2 מספר עם – 1. במקרה זה, -2 2-1 = -2 1 = -2. אין 2+ בטווח של המספרים המשלימים של שניים ב-2 ביטים.
| טבלה 3.32 המספרים השלמים של Two בארבעה ביטים |
|
|---|---|
| בינארי | נקודה |
| 0111 | +7 |
| 0110 | +6 |
| 0101 | +5 |
| 0100 | +4 |
| 0011 | +3 |
| 0010 | +2 |
| 0001 | +1 |
| 0000 | +0 |
| 1111 | -1 |
| 1110 | 1110 |
| 1101 | -3 |
| 1101 | -3 |
| 1100 | -4 |
| 1011 | -5 |
| 1010 | -6 |
| 1001 | 1001 |
| 1000 | -8 |
המספרים הבינאריים החיוביים הם מ-0000 עד 0111 (כלומר מאפס עד שבע). בחלק השמאלי ביותר, אפס מראה שהם מספרים חיוביים. 0000 הוא קצת באמצע הטווח. כדי לקבל -1, נמצא שההיפוך של המספר 0001 הוא 1110. הוספת 1 לזה (בקצה הימני) נותן 1111. כדי לקבל -2, ההיפוך של 0010 נמצא 1101. הוספת 1 לזה ( מהימין הקיצוני) נותן 1110. שאר המספרים הבינאריים השליליים כמו -3 עד -7 נקבעים באופן דומה.
מכיוון שמשתמשים בארבע סיביות, נותרו שלוש סיביות לייצג את המספרים בטווח שהם +7, +6, +5, +4, +3, +2, +1, +0, -1, -2, - 3, -4, -5, -6 ו-7 המקבילים ל-0111, 0110, 0101, 0100, 0011, 0010, 0001, 0000, 1111, 1110, 1101, 1100, 1011, 1011, ו-1.
יש להתייחס ל-8 שמתאים ל-1000 בנפרד. הסיבית הראשונה עבור כל המספרים הללו מציינת את הסימן 0 עבור מספרים חיוביים ו-1 עבור מספרים שליליים. קורה ש-1000 אינו בין ארבעה עשר המספרים הבינאריים הללו. 1000 מתחיל ב-1 מה שאומר שהוא חייב להיות מספר שלילי, בכל הנוגע להשלמה של שניים. אז, 1000 נכלל בטווח, כלומר -8.
עם ארבע ביטים בהשלמה של שניים, המספר של כל המספרים השלמים (חיוביים ושליליים) שניתן לייצג הוא 2 4 = 16 ולא 2 4 – 1 = 15. הניואנס נובע מהכללת המספר השלילי האחרון שהוא השלילי של 2 מספר רוחב – 1. במקרה זה, -2 4 -1 = -2 3 = -8. אין 8+ בטווח המספרים.
ניתן ליישם את הניתוח הקודם עבור שניים, ארבע וסיביות רחבים יותר בהשלמה של שניים על מספרים בינאריים ברוחב של 8 סיביות, 16 סיביות, 32 סיביות ו-64 סיביות.
המשלים של שני מקריב את הסיביות הראשונה (הכי שמאלית) עבור הסימן 0 עבור מספר חיובי ו-1 עבור מספר שלילי. עבור קבוצת הביטים הרחבה של 'n' סיביות, יש 2 נ סך הכל חיובי פלוס מספרים שליליים. זה יהיה 2 נ -1, לולא המספר השלילי האחרון (הקטן ביותר) המזל שכלול. המספר החיובי הגבוה ביותר הוא +2 n-1 -1 והמספר השלילי הקטן ביותר הוא -2 n-1 -1. זה יהיה -2 n-1 -1, לולא בני המזל -2 n-1 כלול.
הפחתת מספרים בהשלמה של שתיים
בחיסור:
A – B = D
A נקרא המינואנד, B נקרא subtrahend, ו-D נקרא ההבדל.
כדי להחסיר מספר בינארי חיובי אחד ממספר בינארי חיובי אחר, ה-minuend נכתב בהשלמה של שתיים והמשנה מומרת לערך המשלים של שתיים שליליות שלו. אז, ההצהרה המתמטית הופכת:
A+ – B = D
במילים אחרות, בחיסור המשלים של שניים, ה-subtrahend מומר למספר שלילי ואז מתווסף ל-minuend.
דוגמה 3.31:
הערך את הביטוי העשרוני הבא בהשלמה של שניים באמצעות ארבע סיביות:
6 - 4
פִּתָרוֹן:
המספר הבינארי עבור 6 הוא 110. בהשלמה של 4 סיביות, הוא 0110. המספר הבינארי עבור 4+ הוא 100. בהשלמה של 4 סיביות שתיים, הוא 0100. 0100 שיש להמיר ל-4 שלילי בשניים משלים באופן הבא: ההשלמה או ההיפוך של 0100 הוא 1011. הוספת 1 לזה מהקצה הימני, כפי שעשינו בנוסף, נותן 1100. אז, הביטוי העשרוני הוא:
6 - 4 שהופך ל:
0110 – 0100 כלומר
0110 +(– 0100) = 0110 + 1100 נעשה כמו בסעיף ההוספה הקודם כמו:

הערה: 0110 +(– 0100) זהה ל-6 + – 4
עם חיסור משלים של שניים, כל נשיאה, לאחר העמודה האחרונה שמאלה, בתוספת, נזרקת. כאשר מחסור בעשרוני, המשפט המתמטי הוא:
6 - 4 = 2
אם עושים את אותו הדבר בהשלמה של שניים, התשובה היא 0010 שזה 2+ בספירה בינארית של שניים. החיסור הקודם מפחית מספר קטן ממספר גדול יותר. בדוגמה הבאה, מספר גדול יותר מופחת ממספר קטן יותר. ניתן לעיין בטבלה 3.32 כדי לראות אם 0010 הוא באמת ההשלמה של שתיים ששווה ערך ל-+2.
דוגמה 3.32:
הערך את הביטוי העשרוני הבא בהשלמה של שניים עם ארבע ביטים:
4 - 6
פִּתָרוֹן:
המספר הבינארי עבור 4 הוא 100. בהשלמה של 4 סיביות שתיים, הוא 0100. המספר הבינארי עבור 6+ הוא 110. בהשלמה של 4 סיביות שתיים, הוא 0110. יש להמיר את 0110 לשלילי 6 בהשלמה של שתיים כדלקמן: ההשלמה או ההיפוך של 0110 הוא 1001. הוספת 1 לזה מהקצה הימני, כפי שעשינו בתוספת הקודמת, נותנת 1010. אז, הביטוי העשרוני הוא:
4 - 6 שהופך ל:
0100 – 0110 כלומר
0100 +(– 0110) = 0100 + 1010 נעשה כמו בסעיף ההוספה הקודם כמו:

הערה: 4+ – 6 זהה ל-0100 +(– 0110).
עם חיסור משלים של שניים, כל נשיאה, לאחר העמודה האחרונה שמאלה, בתוספת, נזרקת. כאשר מחסור בעשרוני, המשפט המתמטי הוא:
4 – 6 = -2
אם עושים את אותו הדבר בהשלמה של שניים, התשובה היא 1110 שהוא -2 בספירה בינארית של שניים. ניתן לעיין בטבלה 3.32 כדי לראות אם 1110 הוא באמת השלמה של שתיים ששווה ערך ל-2.
3.4 הכפל של מספרים בינאריים
בהצהרה:
A x B = P
A נקרא מכפיל, B נקרא מכפיל ו-P נקרא מכפלה. הביטוי A x B פירושו להוסיף A, B מספר פעמים כאשר A ו-B הם מספרים שלמים (מספרים שלמים).
הכפל בבינארי זהה לכפל בעשרוני. עם זאת, במקום לעשות זאת בעשרוניות, זה נעשה בבינארי. הכפלת הביטוי העשרוני של 42 על 10 מתבצעת בבינארי באופן הבא כאשר 42 10 = 101010 2 ו-10 10 = 1010 2 :
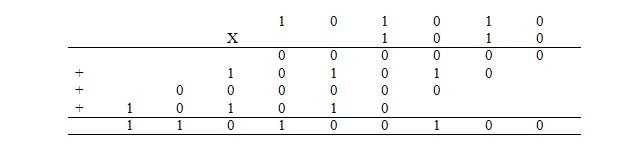
4 המספרים שנוספו נקראים מוצרים חלקיים. התשובה היא המוצר. הוספת המוצרים החלקיים נעשית באותו אופן כפי שהוסבר קודם לכן.
ניתן לראות את הכפל גם כך: בכפל בסיס שני זה, אם הסיבית (הספרה) במכפיל היא 1, הסיבית הפחות משמעותית של המכפלה החלקית שלו היא הסיבית הפחות משמעותית של הכפל אשר מוקלדת ישירות מתחתיה; ושאר הסיביות של הכפיל חוזרים שמאלה. בכפל בסיס שני זה, אם הסיביות (הספרה) במכפיל היא 0, המכפלה החלקית שלו מורכבת מ-0 עם הסיבית הכי פחות משמעותית של 0 ישירות מתחתיה. המספר של כל האפסים הוא מספר הסיביות במכפיל.
3.5 חלוקה של מספרים בינאריים
בהצהרה:
A ÷ B = Q
A נקרא הדיבידנד, B נקרא המחלק, ו-P נקרא הכמות. המנה עשויה להיות מלווה בשארית. הביטוי A ÷ B פירושו כמה פעמים ניתן להוסיף את B כדי לתת A או להיות קרוב אליו כך שהשאר הוא 0 או פחות מ-B.
חלוקה יכולה להתבצע בדרכים רבות. החלוקה שמוצגת כאן היא חטיבת השיקום.
שיקום חטיבה
זוהי שיטת החלוקה הארוכה הנלמדת בבתי הספר. אם 237 מחולק ב-6, התשובה היא 39 השארית 3. ה-237 10 בבסיס 2 הוא 11101101 2 ו-6 10 בבסיס 2 הוא 110 2 . ה-39 10 בבסיס 2 הוא 100111 2 ו-3 10 בבסיס 2 הוא 11 2 .
אז, 11101101 2 חלקי 110 2 נותן 100111 2 השאר 11 2 בבסיס שני. בשיטת השחזור, המספרים הבינאריים הם מספרים רגילים והם לא בהכרח בהשלמה של שניים. המבנה הבא מחלק את 11101101 2 עד 110 2 לתת 100111 2 השאר 11 2 :

חיסור נעשה באופן רגיל ולא באמצעות המשלים של השניים. מכיוון שמדובר בבסיס שני, הלוואה היא שתיים ולא עשר. הדיבידנדים החלקיים הם 10, 101, 1011, 1010 ו-1001. 11 הוא היתרה. מכיוון שלמחלק יש שלוש ספרות, החלוקה מתבצעת בעצם בקבוצות של שלוש ספרות מהדיבידנד הנתון. המנה היא המספר השלם (מספר שלם), והיא 100111 עבור בעיה זו. התוצאה של המנה והשאר היא כצפוי.
3.6 פעולות אריתמטיות עם תוכנה וחומרה
ללוח האם של המחשב יש שעון. תקתוקי השעון נקראים פולסים. בכל פעימת שעון מתקבלת החלטה אחת או יותר במקומות שונים בלוח האם; וזה קשור לתכנות (תוכנה).
בתוך המיקרו-מעבד, ישנם שני סוגים של מעגלים הנקראים: מעגלים לוגיים משולבים ומעגלים לוגיים רציפים. יש סוג אחר של מעגל שנקרא מרובה. חיבור, כפל וחילוק יכולים להתרחש בתוך מרווח שעון אחד באמצעות הלוגיקה השילובית (מעגל). בעוד תכנות (תוכנה) מחייבת החלטה בכל דופק שעון באמצעות מעגלים לוגיים רציפים ומרבבים.
כאשר החיסור מתבצע באמצעות המשלים של שני, יש צורך בשני פולסי שעון לפחות. בדופק השעון הראשון, מרובה מתעל את ה-subtrahend לקבוצה של שערים NOT (שער NOT אחד לכל ספרה). בפולס השעון השני, הלוגיקה השילובית מוסיפה 1 לפלט של שערי NOT וממשיך להוסיף את ה-subtrahend וה-minuend המתקבלים. כל התוספת הזו יכולה להתרחש בתוך מרווח שעון אחד.
חיבור, כפל וחילוק עדיין יכולים להיות מופחתים עם תכנות באמצעות טבלאות האמת. עם זאת, זה לא מכוסה בקורס קריירה מקוון זה.
3.7 פעולות לוגיות במיקרו-מעבד
AND, OR, XOR ו- Invert
ו
הטבלה הבאה ממחישה את Bitwise AND. המשמעות היא שעבור שני מספרים בינאריים שונים, הסיביות התואמות מסומנות ב-AND בהתבסס על טבלת AND Truth:
נע משמאל לימין, 1 ו-1 = 1; 0 ו-1 = 0; 0 ו-0 = 0; 1 ו-0 = 0; וכן הלאה בהתאם ל-AND Truth Table.
אוֹ
הטבלה הבאה ממחישה את OR Bitwise. משמעות הדבר היא שעבור שני מספרים בינאריים שונים, הסיביות המתאימות עוברות OR על סמך טבלת OR Truth:

נע משמאל לימין, 1 או 1 = 1; 0 או 1 = 1; 0 או 0 = 0; 1 או 0 = 1; וכן הלאה בהתאם לטבלת האמת של OR.
חינם
הטבלה הבאה ממחישה את ה-Bitwise בלעדי-OR. המשמעות היא שעבור שני מספרים בינאריים שונים, הסיביות התואמות עוברות XOR על סמך טבלת האמת XOR:

נע משמאל לימין, 1 XOR 1 = 0; 0 XOR 1 = 1; 0 XOR 0 = 0; 1 XOR 0 = 1; וכן הלאה בהתאם ל-XOR Truth Table.
הפוך (לא)
הטבלה הבאה ממחישה את Bitwise NOT (היפוך). המשמעות היא שעבור מספר בינארי אחד, הפעם, כל ביט מתהפך על סמך טבלת ה- NOT Truth:

נע משמאל לימין, לא 1 = 0; NOT 0 = 1; NOT 0 = 1; NOT 1 = 0; וכן הלאה בהתאם ל- NOT Truth Table.
העברה ימינה או שמאלה
העבר ימינה
המספר הבינארי הבא מוזז 3 מיקומי סיביות ימינה, כאשר האפסים מוכנסים למיקומי הסיביות שהתפנו משמאל:

ההסטה יכולה להתבצע עבור מקום אחד, שניים, שלושה, ארבעה וכו'.
העבר שמאלה
המספר הבינארי הבא מוזז 3 מיקומי סיביות שמאלה, כאשר האפסים מוכנסים למיקומי הסיביות שהתפנו מימין:

ההסטה יכולה להתבצע עבור מקום אחד, שניים, שלושה, ארבעה וכו'.
סיבוב ימינה או שמאלה
סיבוב דומה להזזה. זה נעשה אחד בכל פעם. כאשר מסתובבים ימינה, הסיביות שעוזבות את הקצה הימני לא נופלות כמו בהסטה; הם מחליפים את החלקים שהתפנו משמאל, בזה אחר זה. כאשר מסתובבים שמאלה, הסיביות שעוזבות את הקצה השמאלי לא נופלות כמו בהסטה; הם מחליפים את החלקים שהתפנו מימין, בזה אחר זה.
לסובב ימינה
המספר הבינארי הבא מסובב 3 מיקומי סיביות ימינה:

הסיבוב יכול להתבצע עבור מקום אחד, שניים, שלושה, ארבעה וכו'.
רורט שמאלה
המספר הבינארי הבא מסובב 3 מיקומי סיביות שמאלה:

הסיבוב יכול להתבצע עבור מקום אחד, שניים, שלושה, ארבעה וכו'.
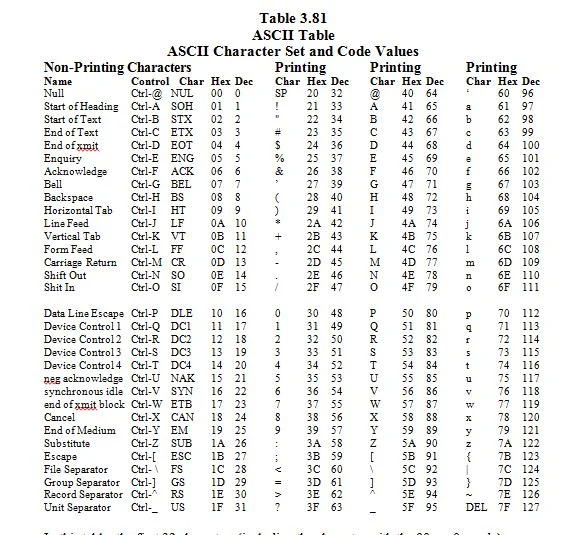
3.8 ערכת תווים ASCII וערכי הקוד שלה
ASCII מייצג 'קוד סטנדרטי אמריקאי (ארה'ב) להחלפת מידע. דמיינו מקלדת עם 96 מקשים. זוהי מקלדת אידיאלית שבה מקשי האותיות הגדולות שונות ממקשי האותיות הקטנות. כל מקש אחר מייצג תו שנמצא על מקלדת אנגלית (ארה'ב). התווים והקודים (המספרים התואמים לתווים) מפורטים ברשימה הבאה:
בטבלה זו, 32 התווים הראשונים (כולל התו עם ה-00 16 = 0 10 קוד) הם תווים שאינם מודפסים. הם דמויות שליטה. הם לא נראים על המסך (מוניטור) שבו הכל שווים. יש להם רק השפעות. בואו נדון יותר על כך מאוחר יותר.
שאר התווים הם תווים מודפסים; הם נראים על המסך. ישנם 128 תווי ASCII. 2 7 = 128. 1,111,111 2 = 127 10 . ה-7 ב-2 7 פירושו 7 ביטים.
עכשיו, 1111111 2 + 1 2 זהה ל:
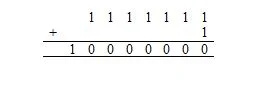
הנה, 10,000,000 2 = 128 10 . יש 128 10 תווים ברשימה הקודמת (טבלה) של תווי ASCII. זה כולל את תו האפס, שהקוד שלו בבסיס שש עשרה (הקסדצימלי) הוא 00, שהוא שווה ערך ל-0 בבסיס עשר.
מכיוון שיש 128 תווים בסך הכל, 128 פחות 32 תווים שאינם מודפסים נותנים 96 תווים מודפסים. בסעיף זה, ההנחה היא שקיימת מקלדת אידיאלית עם 96 תווים שהם תווים להדפסה. במקלדת האידיאלית הזו, המקשים לתווים באנגלית שונים מהמקשים של התווים הקטנים באנגלית.
כל תו במקלדת מיוצג על ידי מספר בסיס שני של 7 ביטים שאינם מוצגים ברשימה. האות הגדולה של 'N', למשל, מיוצגת על ידי שבעת הסיביות 1001110 בבסיס 2. כדי להמיר 1001110 2 לבסיס 16, קדם לו 0 וקבץ את התוצאה בתת-קבוצות של ארבע סיביות באופן הבא:
| 0100 | 1110 | 2 = | 4 | ה | 16
כלומר 01001110 2 = 4E 16 . כדי להמיר 4E 16 לבסיס עשר, בצע את הפעולות הבאות:
4 x (16) 1 + E x (16) 0 = 4 x 16 + E x 1 = 4 x 16 + 14 x 1 = 64 + 14 = 78 10
בצד ימין של 'N' ברשימה (טבלה) מופיע המספר ההקסדצימלי של 4E והמספר העשרוני של 78.
כדוגמה נוספת, התו '[' מיוצג על ידי שבעת הסיביות 1011011 בבסיס 2. כדי להמיר 1011011 2 לבסיס 16, קדם לו 0 וקבץ את התוצאה בתת-קבוצות של ארבע סיביות באופן הבא:
| 0101 | 1011 | 2 = | 5 | ב | 16
כלומר 01011011 2 = 5B 16 . כדי להמיר 5B16 לבסיס עשר, בצע את הפעולות הבאות:
5 x (16) 1 + B x (16) 0 = 5 x 16 + B x 1 = 5 x 16 + 11 x 1 = 80 + 11 = 91 10
בצד ימין של '[' ברשימה (טבלה) מופיע המספר ההקסדצימלי של 5B והמספר העשרוני של 91.
כדוגמה נוספת, התו עבור המספר העשרוני של '5' מיוצג על ידי שבעת הסיביות 0110101 בבסיס 2, ו לֹא 0000101 בבסיס 2. כדי להמיר 0110101 2 לבסיס 16, קדם לו 0 וקבץ את התוצאה בתת-קבוצות של ארבע סיביות באופן הבא:
| 0011 | 0101 | 2 = | 5 | ב | 16
כלומר 00110101 2 = 35 16 . כדי להמיר 3516 לבסיס עשר, בצע את הפעולות הבאות:
3 x (16) 1 + 5 x (16) 0 = 3 x 16 + 5 x 1 = 3 x 16 + 5 x 1 = 48 + 5 = 53 10
בצד ימין של '5' ברשימה (טבלה) מופיע המספר ההקסדצימלי של 35 והמספר העשרוני של 53.
מכיוון שהמחשב עובד בבתים, כאשר מקש במקלדת האידיאלית נשלחים שמונה ביטים למיקרו-מעבד (לוח האם). המקלדת האידיאלית היא ציוד היקפי המופרד מיחידת המערכת (הבסיס) של המחשב. יש לו מעגל אלקטרוני (IC) שיוצר את שבעת הביטים ומקדים לו אפס לפני שהוא שולח אותו דרך הכבל שלו ללוח האם של יחידת המערכת. מיציאת הקלט (מעגל הקלט) של לוח האם, הוא עובר למיקרו-מעבד שנמצא גם הוא בלוח האם. מהמיקרו-מעבד הוא עובר לזיכרון המותקן גם בלוח האם.
לכן, כאשר מקש 'N' במקלדת האידיאלית נלחץ, שמונה סיביות 01001110 נלקחות למיקרו-מעבד. מהמיקרו-מעבד הם נלקחים לזיכרון שם הם נשארים במיקום זיכרון כבייט. על מתכנת המחשבים לזכור כי שמונה הביטים של 01001110 2 זהה ל-4E 16 שזה זהה ל-78 10 .
כאשר מקש '[' במקלדת האידיאלית נלחץ, שמונה סיביות 01011011 נלקחות למיקרו-מעבד. מהמיקרו-מעבד הם נלקחים לזיכרון שם הם נשארים במיקום זיכרון כבייט. על מתכנת המחשבים לזכור כי שמונה הביטים של 01011011 2 זהה ל-5B 16 שזה זהה ל-91 10 .
כאשר מקש '5' במקלדת האידיאלית נלחץ, בתור תו ולא כמספר עשרוני, שמונה סיביות 00110101 נלקחות למיקרו-מעבד. מהמיקרו-מעבד הם נלקחים לזיכרון שם הם נשארים במיקום זיכרון כבייט. על מתכנת המחשבים לזכור כי שמונה הביטים של 00110101 2 זהה ל-35 16 שזהה ל-5310 10 .
יש מקרים שבהם תוכנית פועלת ומחכה להזנת המספר העשרוני של 5 למחשב. במצב זה, אם מקש '5' במקלדת האידיאלית נלחץ, עדיין קוד שמונה הסיביות של 00110101 נלקח למיקרו-מעבד. מכיוון שמה שצריך הוא המספר העשרוני של 5, ולא התו '5', קטע קוד (תוכנית קצרה) מהזיכרון משתמש במיקרו-מעבד כדי להמיר את קוד התו של 00110101 בבסיס שני למספר המשלים של השניים 00000101 2 לפני שליחתו למיקום זיכרון בתור בתים משלימים של שני. מתכנת המחשבים צריך לזכור ש-00000101 פירושו 5 10 בבסיס 2, והוא שונה ממספרי הקוד של 00110101 2 , 35 16 , ו-53 10 שפירושו התו של '5'. על מנת להציג את המספר המשלים של השניים 00000101 בזיכרון, תוכנית קצרה נוספת צריכה להמיר 00000101 מהזיכרון ל-00110101. זה 00110101 שזהה ל-35 16 שזה זהה ל-53 10 שמוצג על הצג (או מודפס על נייר על ידי המדפסת).
3.9 פורמט מספרי נקודה צפה
מספר ללא חלק עשרוני הוא מספר שלם. המספר 36 הוא מספר שלם. 36.375 אינו מספר שלם. זהו מספר עשרוני עם חלק עשרוני. החלק העשרוני של .375 הוא שבר שהוא פחות מ-1.
36.375 מתפרש בצורה עשרונית כ:
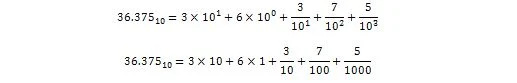
עַכשָׁיו:
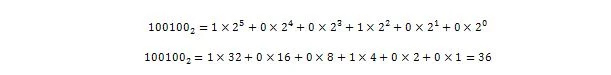
אז, 100100 2 = 3610 שהוא חלק המספר השלם של 36.375 10 .
עַכשָׁיו:
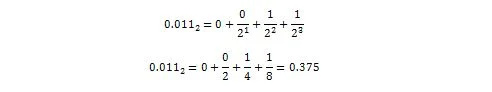
אז, 0.011 2 = 0.375 10 שהוא חלק המספר העשרוני של 36.375 10 .
∴ 36,375 10 = 100100.011 2
נסח את זה אחרת:
100100.011 2 = 36,375 10
המספרים מיוצגים במחשב בבסיס 2 ולא בבסיס 10, כשהכל שווה. מכיוון שתא ברישום במיקרו-מעבד או תא בזיכרון יכולים לקחת רק 1 או 0, אין מקום לאחסן נקודה עשרונית. זה מעורר בעיה. כרזולוציה, יש את ייצוג הנקודה הצפה 32 סיביות דיוק יחיד IEEE-754 ואת ייצוג הנקודה הצפה 64 סיביות דיוק כפול IEEE-754.
פורמט מספרי נקודה צפה 32 סיביות
ניתן לבטא את המספר 100100.0112 כך:
100100.011 2 = 1.00100011 2 x 2 +5
הצד הימני של הסמל = מכונה במתמטיקה כצורת הבסיס שתיים הסטנדרטית של הצד השמאלי של 100100.011 2 .
כעת, 00100011 מתוך 1.00100011 2 בצד ימין של הסמל =, ללא ה-'1' הקודם. וללא ה-2 עבור הבסיס, נקרא המשמעות המפורשת. במקרה זה, הנקודה הבינארית נלקחת חמישה מקומות שמאלה כדי לקבל את ה'1'. אל תבלבלו בין נקודה עשרונית לנקודה בינארית. נקודה בינארית היא עבור בסיס 2, בעוד שנקודה עשרונית היא עבור בסיס 10. ה-'1'. ואחריו 00100011 בצד ימין של הסמל =, ללא ה-2 עבור הבסיס, יוצרים את המשמעות האמיתית. עם זאת, 1.00100011 נקרא המשמעות המרומזת.
אחרי הסימן בצד ימין מופיע הסימן 'x 2 +5 ' ביטוי. עם ביטוי זה, ה-+5 נקרא המעריך. סימן הפלוס אומר שיש להזיז את הנקודה הבינארית חמישה מקומות קדימה כדי להיות במיקום המקורי הרגיל שלה ו-2 הוא הבסיס למספור. ניתן לכתוב את המשוואה הקודמת הפוך כך:
1.00100011 2 x 2 +5 = 100100.011 2
עם ייצוג הנקודה הצפה של 32 סיביות, הוא '1.00100011 2 x 2 +5 ' שמשמש ולא רק '100100.011 2 '. ה-2 עבור הבסיס אינו רשום. ייצוג הנקודה הצפה של 32 סיביות עבור '1.00100011 2 x 2 +5 ” מספר, השווה ל-36.375 10 = 100100.011 2 , מוצג בטבלה הבאה:

יש מיקומי 32 סיביות הממוספרים מהקצה הימני, מתחילים מ-0. הסיביות הראשונה בקצה השמאלי היא סיבית הסימן. אם המספר חיובי, סיביות זו היא 0. אם המספר שלילי, סיביות זו היא 1 (-1 מורכב משני תווים ואי אפשר לשים אותו בכל תא אחד). ה-1.00100011 2 x 2 +5 שזה שווה ל-36.375 10 שהוא גם שווה ל-100100.011 2 הוא מספר חיובי. אז, הסיביות הראשונה היא 0.
יש שמונה מיקומי סיביות עבור המעריך, החל ממיקום 30 ועד למיקום 23, כולל. עם זאת, המעריך שנכתב שם הוא 10000100 2 שהוא שווה ל-132 10 . המעריך של מספר הריבית הוא למעשה +5 של הבסיס של שניים. אז מה קורה?
כעת, בפורמט 32 סיביות, מעריך של 0 נכתב כ-01111111 2 שהוא שווה ל-127 10 . ה-+5 10 הוא +101 2 . אז, כשהגענו ל-10000100 2 בחלק המעריך בטבלה, 101 2 נוסף ל-01111111 2 , בהתאם. זה אומר ש-5 נוסף ל-127 כדי לקבל 132 10 .
המשמעות, ללא '1', הורידה את עמדות 22 ל-15, כולל. שים לב שה-1 של '1'. לא צוין במחרוזת 32 סיביות. זה אף פעם לא מצוין - קבל את זה. שאר התאים עד למיקום 0 מלאים באפסים.
אם המעריך בפועל הוא -5, אז 5 מופחת מ-127 10 שיהיה 122 10 . זה מתאים להפחתת 101 2 מ-01111111 2 שיהיה 01111010 2 .
עם כל האיור הקודם, המספר +1 השווה ל-1.0 x 2 0 = 1.0 x 1 = 1.0 מיוצג כ:

שימו לב שה-'1'. של 1.0 x 2 0 לא מצוין בפורמט. זה אף פעם לא מצוין. השבר המעורב הבא שהולך חיובי אחרי 1.0 הוא:

שימו לב ל-1 בקצה הימני. ייצוג זה הוא המספר:

ההבדל בין 1.0000001192092896 ל-1.0 הוא:
1.0000001192092896 – 1.0 = 0.0000001192092896
המספרים עם חלקים עשרוניים הם שברים מעורבים. לא כל השברים בין 1 10 ו-2 10 יכול להיות מיוצג במחשב. ניתן להניח שהפער השברי הקטן ביותר בין המספרים המעורבים הרצופים בפורמט הנקודה הצפה של 32 סיביות הוא 0.0000001192092896. צפו שהמרווח עבור דיוק כפול יהיה קטן יותר. עיין באיור הבא.
המייצג את המספר, 0.0 אינו עוקב אחר הטיעונים הקודמים. הייצוג של 0.0 מוכרז ויש ללמוד אותו ככזה. כדי לייצג 0.0, כל התאים עבור המובהק הם 0 וכל התאים עבור המעריך הם גם אפס. סיביות הסימן יכולה להיות 0 או 1. למרבה הצער, זה גורם ל-0 חיובי ול-0 שלילי באופן הבא:

בחיים האמיתיים, יש רק אפס אחד. 0 חיובי ו-0 שלילי לא קיימים. עם זאת, 0 נחשב בדרך כלל כחיובי. 0 חיובי ושלילי 0 קיימים כאן בגלל תיאור הפורמט המסוים הזה. לקו המספרים (ראה לעיל) יכולים להיות גם +0 ו-0, אך קיים רק אפס אחד.
פורמט מספרי נקודה צפה 64 סיביות
פורמט הנקודה הצפה של 64 סיביות דומה לפורמט 32 סיביות, אך עם ההבדלים הבאים:
- יש 64 סיביות לייצג מספר.
- אחרי סיביות הסימן, יש 11 סיביות למספר המעריך.
- מספר המעריך עבור אינדקס אפס (2 0 ) הוא 1023 10 = 01111111111 2 .
- אחרי אחד-עשר הסיביות מופיעות 52 סיביות עבור המשמעות המפורשת.
- יש לו מגוון רחב יותר של מספרים מאשר בפורמט 32 סיביות.
שימו לב שה-'1'. שזה בתחילת ה-significand עדיין לא נכלל בין 64 הסיביות, בדיוק כפי שהוא לא נכלל בין 32 הסיביות עבור פורמט 32 הסיביות.
אחד ההבדלים החשובים ביותר בין פורמט 64 סיביות לפורמט 32 סיביות הוא שההבדל בין השברים המעורבים הרצופים בפורמט 64 סיביות קטן מזה של פורמט 32 סיביות.
בפורמט 64 סיביות, ניתן לחשב את המרווח (הפער) בין 1.0 לשבר המעורב הבא באופן הבא:
1.0 הוא
0 01111111111 000000000000000000000 00000000000 0000000000000000000 2
זה שווה ערך ל'1', שלא צוין במחרוזת, כפול 2 המועלה בחזקת (אינדקס) 0 (כאשר המעריך הוא 1023 10 = 01111111111 2 עבור 2 0 = 1). המיתר הוא 1.0 על 2 0 .
השבר המעורב הבא הגדול מ-1.0 הוא:
0 01111111111 0000000000000000000000 000000000000 000000000000000000000000 2
זה שווה ערך ל'1'. שאינו מצוין במחרוזת, ואחריו 51 אפסים, ולאחר מכן 1, כפול 2 מועלה בחזקת 0 (כאשר המעריך הוא 1023 10 = 011111111112 2 עבור 2 0 = 1). זה זהה ל:
+2 0 × (1 + 2- -52 ) ≈ 1.00000000000000002
ה- ≈ פירושו שווה בערך ל.
עַכשָׁיו:
1.00000000000000002 – 1.0 ≈ 0.00000000000000002
ערך המרווח המתאים עבור פורמט של 32 סיביות הוא 0.0000001192092896 ≈ 0.00000012.
0.00000000000000002 קטן בהרבה מ-0.00000012. לכן, ישנם הרבה יותר שברים מעורבים בין שני מספרים שלמים עוקבים (למשל 3 ו-4) בפורמט 64 סיביות מאשר יש בין שני מספרים שלמים עוקבים עבור פורמט 32 סיביות.
מספר השברים המעורבים בין שני מספרים שלמים עוקבים על קו המספרים הוא אינסופי. לכן, שום פורמט (למשל 32 סיביות או 64 סיביות) לא יכול לספק את כל השברים המעורבים בין שני מספרים שלמים עוקבים (מספרים שלמים). ככל שהפער (מרווח) קטן יותר בין שני מספרים שלמים עוקבים המסופקים על ידי פורמט (למשל 32 סיביות או 64 סיביות), כך גדל מספר השברים המעורבים בין המספרים השלמים העוקבים (עבור קו המספרים).
הסיבות לכך שפורמט 64 סיביות מתואר כדיוק כפול או גבוה יותר, בהשוואה לפורמט 32 סיביות, הן שהמרווח בין שני שברים מעורבים עוקבים התחום על ידי שני מספרים שלמים עוקבים עבור פורמט 64 סיביות קטן מ-32 המקביל - מרווח פורמט סיביות. כמו כן, ישנם יותר שברים מעורבים אפשריים בין שני מספרים שלמים מוגבלים עבור פורמט 64 סיביות מאשר בהתאמה עבור פורמט 32 סיביות.
המרת חלק עשרוני (שבר) של מספר עשרוני לחלק בינארי
ה-36.375 הוא מספר עשרוני עם החלק העשרוני של '.375'. החלק העשרוני של '.375' הוא שבר בין אפס לאחד. ה-0.5 בבסיס עשר זהה בערכו ל-1/2 בבסיס שני. ה-0.5 10 שמתבטא בהרחבת הבסיס שתיים היא:
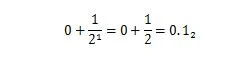
זה לא 0.101 2 כלומר 0.625 10 . לחלק העשרוני של מספר עשרוני יש את החלק הבינארי המקביל שלו למספר הבינארי המקביל. אז, כדי להמיר מספר עשרוני כמו 36.375 10 לבסיס שני, המר 36 לבינארי ואז המר את .375 גם לבינארי. לאחר מכן, חבר את שתי התוצאות עם הנקודה הבינארית. השיטות להמרת שני הסעיפים שונות. כיצד להמיר מספר שלם עשרוני לבסיס 2 מוסבר בפרק 1.
כדי להמיר את השבר העשרוני לשבר בינארי, בצע את השלבים הבאים:
- הכפל את השבר העשרוני (החלק העשרוני) ב-2. המספר השלם הנובע מכך הוא הספרה הבינארית הראשונה.
- חזור על השלב הקודם עם התוצאה השברית העשרונית כדי לקבל את הספרה הבינארית הבאה.
- המשך לחזור על השלב הקודם עד שתוצאת השבר העשרוני תהיה 0.0000—.
דוגמה: המר את החלק השבר של 36.375 10 לחלק השבר המקביל בבסיס שני.
פִּתָרוֹן:
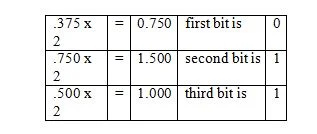
שים לב שבשלב השלישי, .500 הוכפל ב-2 ולא ב-1.500. השבר הבינארי המקביל נקרא בעמודה האחרונה מלמעלה. וכך, התוצאה הבאה היא:
.375 10 = .011 2
המרת חלק בינארי (שבר) של מספר בינארי לחלק עשרוני
כדי להשיג זאת, הרחב את השבר הבינארי בחזקות הדדיות של 2.
דוגמה: המר את החלק השברי של 100100.011 2 לחלק השבר המקביל בבסיס עשר.
פִּתָרוֹן:
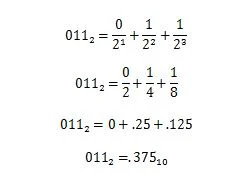
3.10 קידומות מספרים במחשוב
בחיים רגילים, 1 קילו פירושו 1000 אשר מקוצר ב-k (אותיות קטנות) כמו ב-1kg. במחשוב, 1 קילו פירושו 2 10 = 1024, אבל מקוצר ב-K (אותיות גדולות) כמו ב-1Kbits. בחיים רגילים, 1 מגה פירושו 1,000,000 אשר מקוצר ב-M (אותיות גדולות) כמו ב-1Mg. במחשוב, 1 מגה פירושו 2 עשרים = 1,048,576 = 2 10 x 2 10 = 1024 x 1024 = 1,048,576 ועדיין מקוצר ב-M (אותיות גדולות) כמו ב-1Mbits. בחיים רגילים, 1 גיגה אומר ש-1,000,000,000 מקוצר ב-G (אותיות גדולות) כמו ב-1Gg. במחשוב, 1 גיגה פירושו 2 30 = 1,073,741,824 = 2 10 x 2 10 x 2 10 = 1024 x 1024 x 1024 = 1,073,741,824 והוא עדיין מקוצר ב-G (אותיות גדולות) כמו ב-1Gbits. הטבלה הבאה נותנת את המשמעות של ארבע קידומות בחיים רגילים ובמחשוב:
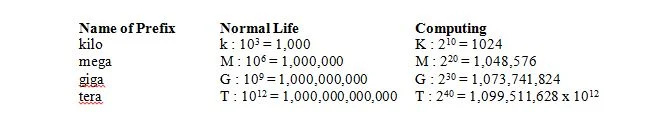
3.11 בעיות
מומלץ לקורא לפתור את כל הבעיות בפרק לפני המעבר לפרק הבא.
- צייר קו מספרים עם מספרים שלמים מ-10 עד +10.
- הוסף את המספרים הבינאריים הבאים בהשלמה של 8 סיביות שתיים: 101010 2 ו-1111 2 .
- השתמש רק בגישת ההשלמה של השניים ב-8 סיביות כדי להחסיר את המספר הבינארי של 1111 2 מהמספר הבינארי של 101010 2 .
- מצא את המוצר של 10110 2 x 1101 2 בבסיס שני.
- מחלקים 36,375 10 עד 1000 10 בעשרוניות ובבינאריות, ולהשוות את התוצאות.
- השתמשו ב-8 סיביות לבחירתכם כדי להמחיש את ההיגיון AND, OR, XOR, Invert, Shift ימינה, Shift שמאלה, סובב ימינה וסיבוב שמאלה. לכל בייט צריך להיות תערובת של 1 ו-0.
- א) כתוב את הקוד המספרי עבור תו ASCII של אפס בהקסדצימלי, בינארי ועשרוני.
ב) כתוב את הקוד המספרי עבור תו ASCII של '1' בהקסדצימלי, בינארי ועשרוני.
ג) כתוב את הקוד המספרי עבור תו ASCII של 'A' בהקסדצימלי, בינארי ועשרוני.
ד) כתוב את הקוד המספרי עבור תו ASCII של 'a' בהקסדצימלי, בינארי ועשרוני. - המרה 49.49 10 לתוך בסיס שני. המר את התוצאה שלך לפורמט IEEE 32-bit נקודה צפה.
- א) במה שונה פורמט הנקודה הצפה של IEEE 64 סיביות מהפורמט של 32 סיביות?
ב) תן את שתי הסיבות הקשורות לכך שהפורמט של 64 סיביות מתואר כדיוק כפול או גבוה יותר על פני
פורמט 32 סיביות.